Напрямки використання прибули на підприємстві (економіко-математичні методи).

Роздивимося напрямки використання прибули на підприємстві за допомогою економіко-математичних методів.

Умова задачі.

Задано таку економічну ситуацію. ВАТ «Орбіта» здійснює складання виробів двох типів А і В. При цьому використовуються комплектуючі чотирьох видів. Витрата комплектуючого кожного виду на виготовлення одиниці виробу і запас комплектуючих задані в таблиці.

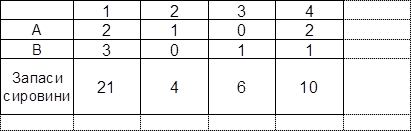
Випуск виробу А приносить 3 грошові одиниці, У - 2 грошові одиниці. Скласти план виробництва, що забезпечує максимальний прибуток.

а) скласти математичну модель задачі; б) пояснити зміст цільової функції й обмежень.

Рішення2:

а) Математична модель.

2х1 + 3х2 £ 21

х1 £ 4

х2 £ 6

2х1 + х2 £ 10

х1 ³ 0

х2 ³ 0

б) Сумарна витрата кожного виду сировини на весь випуск не повинний перевищувати заданого обмеження.

в) Вирішити задачу симплексним методом.

Перетворимо нерівності в рівності, для цього введемо чотири додаткові перемінні.

2х1 + 3х2 + х3 = 21 х1 + х4 = 4 х2 + х5 = 6

2х1 + х2 + х6 =10

f = 3х1 + 2х2 + 0´х3 + 0´х4 + 0´х5 + 0´х6 Þ max

перепишемо у виді систем 0 рівнянь

0 = 21 - (2х1 + 3х2 + х3)

0 = 4 - (х1 + х4)

0 = 6 - (х2 + х5)

0 = 10 - (2х1 + х2 + х6)

f = 0 - (-3х1 - 2х2 - 0´х3 - 0´х4 - 0´х5 - 0´х6)

Система рівнянь може бути записана у виді векторної рівності:

0 = У - (А1х1 + А2х2 + А3х3 + А4х4 + А5х5 + А6х6)

В - вільні члени

А1 . А6 коефіцієнти при перемінних х1 .х6

Лінійна форма має вид:

f = с1х1 + с2х2 + с3х3 + с4х4 + с5х5 + с6х6

Вектори А3, А4, А5, А6 складають базис.

Складаємо першу симплекс таблицю:

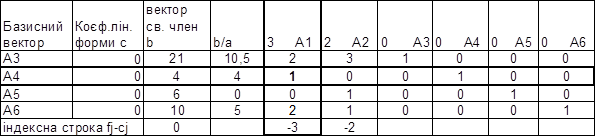
Рішення: х1 = 0, х2 = 0, х3 = 21, х4 = 4, х5 = 6, х6 = 10

f = 0

Тому що в індексному рядку є негативні елементи - рішення не є оптимальним.

А1 вводимо в базис замість вектора А4

Рішення: х1 = 4, х2 = 0, х3 = 13, х4 = 0, х5 = 6, х6 = 2

f = 12

Тому що в індексному рядку є негативні елементи - рішення не є оптимальним.

А2 вводимо в базис замість вектора А6

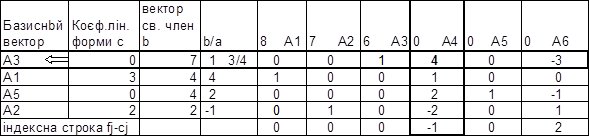
Рішення х1 = 4, х2 = 2, х3 = 7, х4 = 0, х5 = 4, х6 = 0

f = 12

Тому що в індексному рядку є негативні елементи - рішення не є оптимальним.

А4 вводимо в базис замість вектора А3

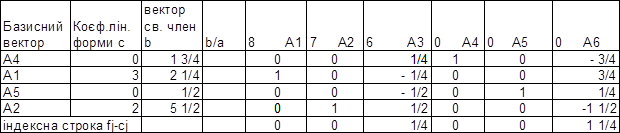
Рішення х1 = 2,25; х2 = 5,5; х3 = 0; х4 = 1 ¾; х5 = ½; х6 = 0

f = 17,75

У індексному рядку немає негативних елементів, отже, подальше збільшення значення лінійної форми неможливо ми одержали оптимальну програму1.

Максимальний прибуток досягається при виготовленні першого виду продукції 2,25 у.о., а другого 5,5 у.о.

Тому що не була задана умова цілочисельності, такі значення припустимі, наприклад, у якості умовних одиниць - тисяч штук.

Подібні статті по економіці

Управління якістю продукції
В умовах переходу до ринку успіх кожного конкретного товаровиробника оцінюється за рівнем ефективності виробництва, зумовленої, насамперед, рівнем задоволення потреб суспільства з найме ...

Державне регулювання підприємництва
Державне регулювання підприємництва є напрямом державної політики, спрямованим на вдосконалення правового регулювання господарських відносин, а також адміністративних відносин між ре ...

Еволюція золота та його роль в сучасних умовах
Якщо на перших етапах розвитку товарного виробництва гроші існували як товар - загальний еквівалент, то гроші і зараз продовжують виконувати функцію загального еквівалента, хоч зі зміною ...