Метод аналітичних груповань

Основні етапи аналізу:. Теоретичне обґрунтування моделі аналітичного групування:

- вибір факторних ознак;

- визначення числа груп k ознаки-фактора xt;

- визначення меж інтервалів групування щодо xt.

Групи мають бути достатньо численні й чисельність груп має бути приблизно однакова.

II. Оцінка лінії регресії:

- визначення частот (частостей) mі у групах;

- розрахунок у кожній групі за факторною ознакою середніх значень результативної ознаки уі.

III. Вимірювання тісноти зв'язку, що ґрунтується на правилі складання дисперсії: загальна дисперсія розпадається на між групову і середню з групових дисперсій і обчислюється за індивідуальними значеннями ознаки у:

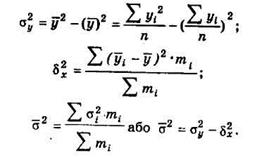
вимірює варіацію у, яка склалася під дією усіх причин;

вимірює варіацію у, яка пояснюється xі,

вимірює варіацію у, яка пов'язана з впливом факторів, крім того, що досліджується;

п - кількість груп;

ті - частота, притаманна кожній з груп за факторною ознакою;

уі - результативна ознака за кожною групою;

у - середня результативна ознака.

Якщо результативна ознака у зовсім не зв'язана з х , то групові середні y не будуть змінюватися зі зміною , тобто дорівнюватимуть одна одній і дорівнюватимуть загальній середній у, а міжгрупова дисперсія буде дорівнювати нулю.

Якщо результативна ознака у функціонально зв'язана з ознакою-фактором , то в кожній групі міжгрупова дисперсія буде дорівнювати нулю, оскільки ознака у середині групи не варіює. Середня з групових дисперсій буде дорівнювати нулю також згідно з правилом складання дисперсій

Тіснота кореляційного зв'язку вимірюється за допомогою кореляційного відношення (емпіричного коефіцієнта детермінації):

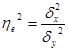- характеризує частку варіації у, яка пояснюється варіацією xt у групі,

де - факторна (міжгрупова) дисперсія;

, - загальна дисперсія.

Якщо

• = 0, то = 0. Це можливо за умови, що всі групові середні однакові й кореляційного зв'язку між ознаками х і у не існує.

• = 1, то , а . У цьому випадку кожному значенню факторної ознаки відповідає єдине значення результативної ознаки, тобто зв'язок між ознаками функціональний.

IV. Перевірка істотності зв'язку, тобто перевірка істотності відхилень групових середніх, яка здійснюється за допомогою критеріїв математичної статистики. Вона ґрунтується на порівнянні фактичного значення з так званим критичним (де - рівень значимості).

є тим максимально можливим значенням кореляційного відношення, яке може виникнути випадково за відсутності кореляційного зв'язку.

Для перевірки істотності зв'язку використовують також функціонально нав'язану з характеристику F-критерій (критерій Фішера) (F).

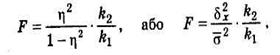
де k1= m - 1; k2 = n-m

де п - кількість одиниць сукупності;

m - кількість груп за х.

Є таблиці критичних значень F-критерію ( , де - рівень значимості).

Якщо , то зв’язок між результативною і факторною ознаками вважається істотним;

якщо , то наявність зв'язку між ознаками не доведено і зв'язок вважається неістотним.

Подібні статті по економіці

Український державний центр транспортного сервісу Ліски
Залізничний транспорт є однією з важливих галузей економіки України, забезпечує її внутрішні та зовнішні транспортно-економічні зв’язки і потребує населення у перевезеннях. Діяльність за ...

Дослідження ефективності функціонування поліграфічного підприємства (на прикладі ЗАТ Віпол)
Актуальність теми даної дипломної роботи є те що на сьогоднішній день питання ефективності функціонування підприємства займає важливу роль. Кожне підприємство щоб вижити на ринку глобал ...

Аграрні відносини та їх розвиток за сучасних умов
Сьогодні сільськогосподарське виробництво і в цілому агропромисловий комплекс України перебувають у центрі суспільної уваги, оскільки і без того небагатий наш стіл останнім часом особливо з ...